Dziś w programie lżejszy zamiennik dla funkcji get_browser() — PHP User Agent. Za pomocą skryptu jesteśmy w stanie określić jakiej przeglądarki i systemu operacyjnego użytkownik używa. Oryginalna funkcja potrzebuje pliku browscap.ini, który obecnie zajmuje 405KB, co przekłada się na szybkość działania. Poza tym istnieje niebezpieczeństwo, że na serwerze produkcyjnym nie dadzą nam dostępu do w/w funkcji. (A przynajmniej tak piszą )

Całość składa się z dwóch klas. Skrypt nie stosuje przestrzeni nazw, za to jest całkiem nieźle udokumentowany. Ponadto jest trochę testów jednostkowych.

Używanie jest bardzo proste. Wystarczy stworzyć obiekt phpUserAgent i można szaleć.

$ua = new phpUserAgent();
echo $ua->getBrowserName();     // firefox
echo $ua->getBrowserVersion();   // 3.6
echo $ua->getOperatingSystem(); // linux
echo $ua->getEngine();            // gecko

Gdy nie podamy parametrów, obiekt korzysta z bieżącej zmiennej $_SERVER['HTTP_USER_AGENT']. Można samemu wymusić inny ciąg do rozpoznania podając w konstruktorze.

Dla typowych konfiguracji użytkownika skrypt działa całkiem nieźle. Rozpoznaje również aliasy nazw przeglądarek i systemów operacyjnych. Z testów jednostkowych widzę, że próbuje również rozpoznawać boty wyszukiwarek.

Patrząc na skrypt przyszłościowo już widzę rozrastającą się listę nazw i aliasów oraz autora powoli przestającego panować nad tym wszystkim. Na razie działa, ale co będzie później? Wg mnie architektura całości jest trochę niedopracowana. Aż prosi się o użycie wzorca projektowego Łańcuch zobowiązań, którego ogniwami będą poszczególne przeglądarki i to w ich gestii będzie rozpoznać siebie w podanym im ciągu. Żeby nie uderzyć tak bardzo w wydajność skryptu, łańcuch powinny rozpoczynać najczęściej używane przeglądarki aż do typu Unknown.

W poprzednim wpisie: Problem przynależności punktu do obszaru wielokąta omówiłem sposoby na sprawdzenie, czy dany punkt należy do obszaru wielokąta rozpiętego na punktach. W tym wpisie przedstawię gotowe rozwiązanie zaimplementowane w PHP. Problem nie jest zbyt rozległy, zatem rozwiązaniem będzie tylko jedna klasa, oraz krótki przykład pokazujący jak z niej korzystać. Do tego jakieś małe demo.

Test przecięć

Do wykonania testu przecięć potrzebna będzie tablica ze współrzędnymi badanego punktu, oraz tablica współrzędnych (podanych w kolejności) wierzchołków wielokąta. Tablice te przekażemy w konstruktorze. Ważną rzeczą jest sprawdzenie czy ostatni i pierwszy element tablicy wierzchołków jest taki sam, czyli czy figura się zamyka. Jeśli nie to w konstruktorze uzupełniamy tablicę kopię pierwszego elementu.

Kolejnym etapem jest sprawdzenie czy punkt należy do do jednego z boków wielokąta. Jeśli powyższe sprawdzenie się nie powiedzie rozpoczynamy właściwą część, tj. sprawdzenie przecięć. W tym celu tworzymy półprostą, tutaj równoległą do osi OX, rozpoczynającą się w sprawdzanym przez nas punkcie, a kończącą się w dowolnym punkcie poza ostatnim punktem wielokąta (najbardziej wysuniętym w kierunku grotu osi OX).

Po utworzeniu półprostej przechodzimy do właściwego badania przecięć. W pierwszej kolejności pod młotek idzie sprawdzenie zawierania się półprostej w jednym z boków wielokąta (rys. 3, rys. 4 w poprzednim wpisie). Aby to sprawdzić musimy przetestować czy kolejne 2 punkty wielokąta należą do tej półprostej. Jeśli tak się zdarzy to sprawdzamy, z którym przypadkiem mamy do czynienia (czy punkty leżą po tej samej, czy po przeciwnych stronach półprostej). Jeśli po przeciwnej – zwiększamy licznik przecięć.

Jeśli półprosta nie zawiera się w boku wielokąta trzeba sprawdzić czy przypadkiem nie przecina jego wierzchołka. Aby to osiągnąć sprawdzamy czy wierzchołek zawiera się w półprostej a zarazem czy poprzedni i następny już nie. Jeśli sprawdzanie się powiedzie to pozostaje rozpoznać, z którą wersją mamy do czynienia (rys. 5, rys. 6 w poprzednim wpisie). W zależności od wyniku, albo zwiększamy licznik przecięć, albo nie. Jeśli natomiast warunek zawierania się wierzchołka nie zostanie spełniony sprawdzamy czy bok wielokąta przecina półprostą, a zarazem poprzedni wierzchołek jej nie przecina, jak również następny.

inPolygon.class.php

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179

<?php
/**
 * @author Robert *Vokiel* Mikołajuk vokiel@vokiel.com http://blog.vokiel.com
 * @copyright (c) 2011 Robert Mikołajuk
 */
class inPolygon {
	/**
	 * @var	array	$point	Współrzędne prawdzanego punktu
	 */
	protected $point;
	/**
	 * @var	array	$raypoint	Punkt końcowy półprostej od $this->point równoległej do osi OX
	 */
	protected $raypoint;
	/**
	 * @var	array	$polygon	Tablica współrzędnych punktów
	 */
	protected $polygon;
	/**
	 * @var	int	$crosses	Liczba przecięć odcinków
	 */
	protected $crosses = 0;
 
	/**
	 *
	 * @param array $point
	 * @param array $polygon
	 */
	public function __construct($point,$polygon){
		$this->point = $point;
		$this->raypoint = array('x' => ($point['x']+1), 'y' => $point['y']);
		$this->polygon = $polygon;
 
		// jeśli ostatni element nie jest tożsamy z pierwszym, dodajemy go na końcu tablicy
		if ( $this->polygon[0] != $this->polygon[count($this->polygon)-1]){
			array_push($this->polygon,$this->polygon[0]);
		}
	}
 
	/**
	 * Sprawdzenie czy punkt zawiera się w obszarze
	 * @return bool
	 */
	public function check(){
		// sprawdzenie czy punkt nie należy do jednego z boków wielokąta
		for ($i=0; $i<count($this->polygon); $i++){
			if ( $this->pointCrossEdge($this->polygon[$i],$this->polygon[$i+1],$this->point) ){
				return true;
			}
		}
 
		$this->setRaypoint();
 
		$this->edgeCross();
 
		if ($this->crosses % 2 == 1){
			return true;
		}
		return false;
	}
 
	/**
	 * Wyznaczenie punktów półprostej równoległej do osi OX
	 * Współrzędna X punktu P1 musi być większa od największej wpsółrzędnej X wśród wszystkich wierzchołków wielokąta
	 */
	protected function setRaypoint(){
		for ($i=0; $i<count($this->polygon); $i++){
			if ( $this->polygon[$i]['x'] > $this->raypoint['x'] ){
				$this->raypoint['x'] = $this->polygon[$i]['x'];
			}
		}
		$this->raypoint['x'] = $this->raypoint['x']+1;
	}
 
	/**
	 * Wyliczenie ilości przecięć półprostej przez odcinki boków wielokąta
	 * Półprosta zostaje przeprowadzona od badanego punktu w prawo,
	 * aż za najbardziej wysunięty w prawo punkt wielokąta
	 */
	protected function edgeCross() {
		// wstawienie na koniec tablicy punktów wielokąta drugiego wierzchołka - dla ułatwienia obliczeń
		array_push($this->polygon,$this->polygon[1]);
		for ($i=0; $i<(count($this->polygon)-1); $i++){
			// Prosta P-P1 zawiera się w boku wielokąta W($i,$i+1) 
			if ($this->pointCrossEdge($this->point, $this->raypoint, $this->polygon[ $i ]) &&
				$this->pointCrossEdge($this->point, $this->raypoint, $this->polygon[ ($i+1) ])
			){
				// Punkt wcześniejszy wielokątea i dalszy leżą po przeciwnej stronie prostej P-P1 - ilość przecięć: 1
				if ($this->sng( $this->det( $this->point, $this->polygon[ $i ], $this->polygon[ ($i-1) ] ) ) !=
					$this->sng( $this->det( $this->point, $this->polygon[ $i ], $this->polygon[ ($i+2) ]))
				){
					$this->crosses++;
				}
			} else { // Prosta P-P1 nie zawiera się w boku wielokąta
				// Prosta P-P1 zawiera wierzchołek W($i)
				if ($this->pointCrossEdge( $this->point, $this->raypoint, $this->polygon[ $i ] ) &&
					!$this->pointCrossEdge( $this->point, $this->raypoint, $this->polygon[ ($i-1) ] ) &&
					!$this->pointCrossEdge( $this->point, $this->raypoint, $this->polygon[ ($i+1) ] )
				){
					// Sprawdzenie położenia wierzhołków sąsiadujących z wierzchołkiem W($i)
					if ($this->sng( $this->det( $this->point, array('x'=>($this->point['x']+1),'y'=>$this->point['y']), $this->polygon[ ($i-1) ] ) ) !=
						$this->sng( $this->det( $this->point, array('x'=>($this->point['x']+1),'y'=>$this->point['y']), $this->polygon[ ($i+1) ] ) )
					){
						$this->crosses++;
					}
				} else {
					// Sprawdzenie czy prosta P-P1 przecina bok wilokąta W($i,$i+1)
					if ( $this->edgeCrossEdge( $this->polygon[ $i ], $this->polygon[ ($i+1) ], $this->point, $this->raypoint) &&
						!$this->pointCrossEdge( $this->point, $this->raypoint, $this->polygon[ ($i-1) ] ) &&
						!$this->pointCrossEdge( $this->point, $this->raypoint, $this->polygon[ ($i+1) ] )
					){
						$this->crosses++;
					}
				}
			}
		}
	}
 
	/**
	 *
	 * Sprawdzenie czy $check_point należy do odcinka ($strt_p|$stop_p)
	 * @param array $strt_p	Punkt startowy odcinka
	 * @param array $stop_p 	Punkt końcowy odcinka
	 * @param array $check_point	Sprawdzany punkt
	 */
	protected function pointCrossEdge($strt_p,$stop_p,$check_point){
		return $this->det($strt_p, $stop_p, $check_point) == 0 &&
			min( $strt_p['x'], $stop_p['x'] ) <= $check_point['x'] &&
			$check_point['x'] <= max( $strt_p['x'], $stop_p['x'] ) &&
			min ( $strt_p['y'], $stop_p['y'] ) <= $check_point['y'] &&
			$check_point['y'] <= max( $strt_p['y'], $stop_p['y'] );
	}
 
	/**
	 * Sprawdzenie czy odcinki $strt_p_1-$stop_p_1 i $strt_p_2-$stop_p_2 przecinają się
	 * @param array $strt_p_1	Punkt startowy pierwszego odcinka
	 * @param array $stop_p_1	Punkt końcowy pierwszego odcinka
	 * @param array $strt_p_2	Punkt startowy drugiego odcinka
	 * @param array $stop_p_2	Punkt końcowy drugiego odcinka
	 */
	protected function edgeCrossEdge($strt_p_1,$stop_p_1,$strt_p_2,$stop_p_2){
		return ($this->sng( $this->det($strt_p_1,$stop_p_1,$strt_p_2) ) != $this->sng( $this->det($strt_p_1,$stop_p_1,$stop_p_2) ) &&
				$this->sng( $this->det($strt_p_2,$stop_p_2,$strt_p_1) ) != $this->sng( $this->det($strt_p_2,$stop_p_2,$stop_p_1) ) ||
				$this->pointCrossEdge($strt_p_1,$stop_p_1,$strt_p_2) ||
				$this->pointCrossEdge($strt_p_1,$stop_p_1,$stop_p_2) ||
				$this->pointCrossEdge($strt_p_2,$stop_p_2,$strt_p_1) ||
				$this->pointCrossEdge($strt_p_2,$stop_p_2,$stop_p_1)
		);
	}
 
	/**
	 * Wyznacznik macierzy kwadratowej stopnia 3
	 * @param array $strt_p
	 * @param array $stop_p
	 * @param array $check_point
	 */
	protected function det($strt_p,$stop_p,$check_point){
		return $strt_p['x'] * ( $stop_p['y'] - $check_point['y'] ) + $stop_p['x'] * ( $check_point['y'] - $strt_p['y'] ) + $check_point['x'] * ( $strt_p['y'] - $stop_p['y']);
		/* druga metoda
		return ($strt_p['x'] * $stop_p['y'] + $stop_p['x'] * $check_point['y'] + $check_point['x'] * $strt_p['y'] - $check_point['x'] * $stop_p['y'] - $strt_p['x'] * $check_point['y'] - $stop_p['x'] * $strt_p['y']);
		*/
	}
 
	/**
	 * Określenie znaku liczby
	 * @param int $x	Liczba
	 * @return int $x
	 */
	protected function sng($x){
		if ( $x == 0 ){
			return 0;
		} else if ( $x > 0){
			return 1;
		} else {
			return -1;
		}
	}
 
}// end of inPolygon class

Na koniec przydałoby się napisać jakieś demo. Wkrótce się pojawi.

W życiu programisty pojawiają się sytuacje, gdy programowanie styka się bardzo blisko z matematyką, w tym przypadku z geometrią. We wpisie postaram się przedstawić sposób na rozwiązanie problemu przynależności punktu do obszaru wielokąta (opisanego przez zbiór wierzchołków).

Geofencing

Ostatnio mam dość mało czasu na pisanie na blogu. Jest to związane przede wszystkim z lenistwem, a w drugiej mierze z mojego udziału w jednym, ciekawym projekcie. Z owym projektem wiąże się dzisiejszy wpis. W aplikacji tej zaplanowaliśmy ciekawą funkcjonalność: geofencing, czyli:

Geofencing is a term utilized primarily in the corporate world that refers to the practice of limiting mobile employees to a specific geographic location by tracking their whereabouts via the technology of a global positioning system (GPS).

W telegraficznym skrócie polega to na wyznaczeniu bezpiecznego obszaru, po którym może poruszać się urządzenie z zainstalowanym modułem GPS.

Zastosowań jest wiele, począwszy od śledzenia pracowników, po zabezpieczenia przesyłek. Przy wszystkich zastosowaniach pojawia się ta sama potrzeba sprawdzenia, czy raportowany z urządzenia GPS punkt znajduje się w obrębie zdefiniowanego obszaru, czy jest już poza nim. Możliwości sprawdzenia przynależności punktu do wielokąta jest wiele.

Przynależność do figury prostej

W najprostszym przypadku prostokąta sprowadza się do prostego, matematycznego porównania współrzędnych wierzchołków i sprawdzanego punktu. Nie wymaga skomplikowanych obliczeń, tym bardziej geometrycznych. Niestety sposób mało przydatny w realnym zastosowaniu. Kazać użytkownikom rysować prostokąty wzdłuż trasy Warszawa – Moskwa może kwalifikować się na nagrodę Worst UX. Dzielenie narysowanego skomplikowanego wielokąta na małe prostokąty, następnie sprawdzanie przynależności punktu do każdego z nich też nie wydaje się optymalnym rozwiązaniem.

Metody dla dowolnego wielokąta

Przeszukując otchłanie Internetu można napotkać rozważania nad różnymi metodami na rozwiązanie tego zagadnienia. Kilka z nich zebrał Eric Haines w artykule Point in Polygon Strategies.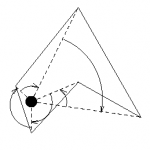

źródło: erich.realtimerendering.com

Suma kątów

Ta metoda polega na zliczeniu sumy kątów liczonych od sprawdzanego punktu do poszczególnych wierzchołków z bokiem wychodzącym z tego wierzchołka. Jeśli suma tych kątów będzie bliska zeru to punkt będzie poza wielokątem, w przeciwnym wypadku będzie do niego należał. Niestety z powodu wykorzystania funkcji trygonometrycznych, konieczności wyznaczenia prostej od każdego wierzchołka do szukanego punktu i wyliczenia dla nich kątów, jest to metoda bardzo powolna.

Czytaj dalej tutaj (rozwija treść wpisu)
Czytaj dalej na blogu autora...

Zwiń
Czytaj na blogu autora...